为图像处理初学者设计的 100 个问题 问题三十一至问题四十
标签(空格分隔): OpenCV
问题三十一至四十
问题三十一:仿射变换(Afine Transformations)——倾斜
- 使用仿射变换,输出(1)那样的$x$轴倾斜$30$度的图像($t_x=30$),这种变换被称为X-sharing。
- 使用仿射变换,输出(2)那样的y轴倾斜$30$度的图像($t_y=30$),这种变换被称为Y-sharing。
- 使用仿射变换,输出(3)那样的$x$轴、$y$轴都倾斜$30$度的图像($t_x = 30$,$t_y = 30$)。
原图像的大小为$h\ w$,使用下面各式进行仿射变换:

Answer
函数AfineTransformations()见上一章
void leanAt(Mat& src, double x_sharing, double y_sharing) {
Mat result = Mat::zeros(src.rows, src.cols, CV_8UC3);
result.forEach<Vec3b>([&](Vec3b& pix, const int * position) {
int x = position[0];
int y = position[1];
int cur_pos[2][1] = { x,y };
Mat m(Size(1, 2), CV_32SC1, cur_pos);
double a_x = x_sharing / src.rows;
double a_y = y_sharing / src.cols;
Mat ori_pos = AfineTransformations(m, 1,a_x,a_y,1, 0, 0);
//printMat(ori_pos);
for (int i = 0; i < 3; i++) {
int ori_pos_x = ori_pos.at<Vec<double, 1>>(0, 0)[0];
int ori_pos_y = ori_pos.at<Vec<double, 1>>(1, 0)[0];
if (ori_pos_x >= src.rows || ori_pos_y >= src.cols || ori_pos_x < 0 || ori_pos_y < 0) {
pix[i] = 0;
}
else
pix[i] = src.at<Vec3b>(ori_pos_x, ori_pos_y)[i];
}
});
src = result;
}Show
Note
-
利用OpenCV的API进行仿射变换
-
第一步:获取仿射映射矩阵(两种)
getAffineTransform() //三点法 Mat M1=getAffineTransform(const Point2f* src, const Point2f* dst) //参数const Point2f* src:原图的三个固定顶点//参数const Point2f dst:目标图像的三个固定顶点
//返回值:Mat型变换矩阵,可直接用于warpAffine()函数
//注意,顶点数组长度超过3个,则会自动以前3个为变换顶点;数组可用Point2f[]或Point2f表示```cpp getRotationMatrix2D //直接指定比例和角度 Mat M2=getRotationMatrix2D (CvPoint2D32f center,double angle,double scale) //参数CvPoint2D32f center,表示源图像旋转中心 //参数double angle,旋转角度,正值表示逆时针旋转 //参数double scale,缩放系数 - 第二步:进行仿射变换
C++ void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar()) //参数InputArray src:输入变换前图像 //参数OutputArray dst:输出变换后图像,需要初始化一个空矩阵用来保存结果,不用设定矩阵尺寸 //参数InputArray M:变换矩阵,用另一个函数getAffineTransform()计算 //参数Size dsize:设置输出图像大小 //参数int flags = INTER_LINEAR:设置插值方式,默认方式为线性插值(另一种WARP_FILL_OUTLIERS) //参数int borderMode=BORDER_CONSTANT:边界像素模式,默认值BORDER_CONSTANT //参数const Scalar& borderValue=Scalar(),在恒定边界情况下取的值,默认值为Scalar(),即0第五个参数插值方式可选方式: 标识符 含义 INTER_NEAREST 最邻近插值 INTER_LINEAR 线性插值(默认) INTER_CUBIC 三次样条插值 INTER_AREA 区域插值 INTER_LANCZOS4 LancZoc4 插值 INTER_LINEAR_EXACT 双线性插值 INTER_MAX 插补码掩码 WARP_FILL_OUTLIERS 填充所有目标图像像素。如果它们中的一些对应于源图像,它们被设置为0 WARP_INVERSE_MAP 逆变换
-
问题三十二:傅立叶变换(Fourier Transform)
使用离散二维傅立叶变换(Discrete Fourier Transformation),将灰度化的imori.jpg表示为频谱图。然后用二维离散傅立叶逆变换将图像复原。
二维离散傅立叶变换是傅立叶变换在图像处理上的应用方法。通常傅立叶变换用于分离模拟信号或音频等连续一维信号的频率。但是,数字图像使用$[0,255]$范围内的离散值表示,并且图像使用$H\times W$的二维矩阵表示,所以在这里使用二维离散傅立叶变换。
二维离散傅立叶变换使用下式计算,其中$I$表示输入图像:
$$
G(k,l)=\frac{1}{H\ W}\ \sum\limits{y=0}^{H-1}\ \sum\limits{x=0}^{W-1}\ I(x,y)\ e^{-2\ \pi\ i\ (\frac{k\ x}{W}+\frac{l\ y}{H})}
$$
在这里让图像灰度化后,再进行离散二维傅立叶变换。
频谱图为了能表示复数$G$,所以图上所画长度为$G$的绝对值。这回的图像表示时,请将频谱图缩放至$[0,255]$范围。
二维离散傅立叶逆变换从频率分量$G$按照下式复原图像:
$$
I(x,y)=\frac{1}{H\ W}\ \sum\limits{l=0}^{H-1}\ \sum\limits{k=0}^{W-1}\ G(l,k)\ e^{2\ \pi\ i\ (\frac{k\ x}{W}+\frac{l\ y}{H})}
$$
上式中$\exp(j)$是个复数,实际编程的时候请务必使用下式中的绝对值形态1:
如果只是简单地使用for语句的话,计算量达到$128^4$,十分耗时。如果善用NumPy的化,则可以减少计算量(答案中已经减少到$128^2$)。
Principe
本节Principe中的内容适合不了解傅里叶变换的读者阅读
傅里叶变换可以将一副图片分解为正弦和余弦两个分量,换言之,它可以将一幅图像从空间域(spatial domain)转换为频域(frequency domain)。这种变换的思想是任何函数可以很精确的接近无穷个sin()函数和cos()函数的和。
我们来梳理一下概念:
- 空间域
一般情况下,空间域的图像是f(x, y) = 灰度级(0-255),形象一点就是一个二维矩阵,每一个坐标对应一个颜色值 - 频率域
对于一个正弦信号,如果它的幅度变化很快,我们称之为高频信号,如果变化非常慢,我们称之为低频信号。迁移到图像中,图像哪里的幅度变化非常大呢?边界点或者噪声。所以我们说边界点和噪声是图像中的高频分量(这里的高频是指变化非常快,不是出现的次数多),图像的主要部分集中在低频分量。
由于图像变换的结果原点在边缘部分,不容易显示,所以将原点移动到中心部分。
那么结果便是中间一个亮点朝着周围发散开来,越远离中心位置的能量越低(越暗)。
对于二位图像其傅里叶变换公式如下:
$$
F(k,l)= \sum\limits{y=0}^{N-1}\ \sum\limits{x=0}^{N-1}\ f(x,y)\ e^{-2\ \pi\ j\ (\frac{k\ x}{N}+\frac{l\ y}{N})}
$$
$$
e^{ix}=cos x+i sin x
$$
式中 f(i, j)是图像空间域的值,F(k ,l)是频域的值。傅里叶转换的结果是复数,这也显示了傅里叶变换是一幅实数图像和虚数图像叠加或者是幅度图像和相位图像叠加的结果。
Answer
toGray()函数在之第一章声明过,也可是使用OpenCV自带的API来转换灰度图-
傅里叶变换
//// Discrete Fourier transformation //这个奇怪的vector就是用来存转换后的频域的 std::vector< std::vector< std::complex<double>>> DFT(Mat& src) { int width = src.cols; int height = src.rows; std::complex<double> val; Mat grey = toGray(src); std::vector<std::vector<std::complex<double>>> FTMap; Mat result = Mat::zeros(width, height, CV_8UC1); //j,k用来表示频谱图中的坐标 for (int j = 0; j < width; j++) { std::vector<std::complex<double>> MapLine; for (int k = 0; k < height; k++) { val.real(0); val.imag(0); //x,y表示时域中的坐标 for (int x = 0; x < width; x++) { for (int y = 0; y < height; y++) { uchar I = grey.at<Vec<uchar, 1>> (x, y)[0]; double theta = (double)-2 * 3.1415926*(((double)k*(double)y / (double)height) + ((double)j*(double)x / (double)width)); val += (double)I*std::complex<double>(cos(theta), sin(theta)); } } val /= sqrt((double)width*(double)height); result.at<Vec<uchar, 1>>(j, k)[0] = (uchar)sqrt(val.imag()*val.imag() + val.real()*val.real()); MapLine.push_back(val); } FTMap.push_back(MapLine); } //输出以下现在是什么样的图案 imshow("FDT", result); return FTMap; } -
傅里叶逆变换
Mat IDFT(std::vector<std::vector<std::complex<double>>> FTMap) { Mat result = Mat::zeros(128, 128, CV_8UC1); int width=128, height = 128; std::complex<double> val; for (int j = 0; j < width; j++) { std::vector<std::complex<double>> MapLine; for (int k = 0; k < height; k++) { val.real(0); val.imag(0); //x,y表示时域中的坐标 for (int x = 0; x < width; x++) { for (int y = 0; y < height; y++) { std::complex<double> G = FTMap[x][y]; double theta = (double)2 * 3.1415926*(((double)k*(double)y / (double)height) + ((double)j*(double)x / (double)width)); val += G*std::complex<double>(cos(theta), sin(theta)); } } result.at<Vec<uchar, 1>>(j, k)[0] = (uchar)(std::abs(val) / sqrt(height * width)); } } return result; -
在main函数中这样调用就可以了
Mat img = imread("G:\\cv\\ImageProcessing100Wen-master\\Question_21_30\\imori.jpg"); imshow("原图", img); imshow("effect",IDFT(DFT(img)));
SHow
-
原图
-
转换后的频域图
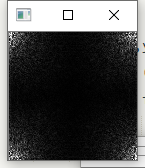
-
逆变换的复原图
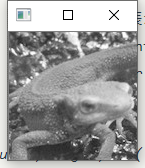
Note
- 可以看到这种方法来求傅里叶变换以及傅里叶逆变换的时间复杂度非常高,达到$O(n^4)$,所以常用的方法是FFT,ji快速傅里叶变换,在之后的题目中会介绍到
问题三十三:傅立叶变换——低通滤波
将imori.jpg灰度化之后进行傅立叶变换并进行低通滤波,之后再用傅立叶逆变换复原吧!
通过离散傅立叶变换得到的频率在左上、右上、左下、右下等地方频率较低,在中心位置频率较高。2
](http://static.zybuluo.com/sliverp/xjivqmgypuebpq9gytx6dz3k/image_1e5fit42n12j1ghj1as76et1eh62g.png)
在图像中,高频成分指的是颜色改变的地方(噪声或者轮廓等),低频成分指的是颜色不怎么改变的部分(比如落日的渐变)。在这里,使用去除高频成分,保留低频成分的低通滤波器吧!
在这里,假设从低频的中心到高频的距离为$r$,我们保留$0.5\ r$的低频分量。
Answer
傅里叶变换和逆变换在前面已经实现过了,这一题直接调用
//低频滤波 Mat LowPassFilter(Mat& src, double pass_r) { auto map = DFT(src); int width = src.cols; int height = src.rows; for (int i = 0; i < width/2; i++) { for (int j = 0; j < height/2; j++) { if (sqrt(i * i + j * j) >= pass_r * height / 2) { map[i][j] = 0; map[width - i-1][j] = 0; map[i][height - j-1] = 0; map[width - i - 1][height - j - 1] = 0; } } } return IDFT(map); }
Show
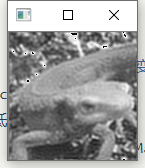
问题三十四:傅立叶变换——高通滤波
将imori.jpg灰度化之后进行傅立叶变换并进行高通滤波,之后再用傅立叶逆变换复原吧!
在这里,我们使用可以去除低频部分,只保留高频部分的高通滤波器。假设从低频的中心到高频的距离为$r$,我们保留$0.2\ r$的低频分量。
Answer
//高通滤波
Mat HighPassFilter(Mat& src, double pass_r) {
auto map = DFT(src);
int width = src.cols;
int height = src.rows;
for (int i = 0; i < width / 2; i++) {
for (int j = 0; j < height / 2; j++) {
if (sqrt(i * i + j * j) <= pass_r * height / 2) {
map[i][j] = 0;
map[width - i - 1][j] = 0;
map[i][height - j - 1] = 0;
map[width - i - 1][height - j - 1] = 0;
}
}
}
return IDFT(map);
}Show
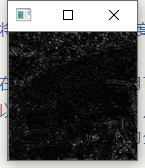
问题三十五:傅立叶变换——带通滤波
将imori.jpg灰度化之后进行傅立叶变换并进行带通滤波,之后再用傅立叶逆变换复原吧!
在这里,我们使用可以保留介于低频成分和高频成分之间的分量的带通滤波器。在这里,我们使用可以去除低频部分,只保留高频部分的高通滤波器。假设从低频的中心到高频的距离为$r$,我们保留$0.1\ r$至$0.5\ r$的分量。
Answer
//带通滤波
Mat BandPassFilter(Mat& src, double pass_start, double pass_end) {
auto map = DFT(src);
int width = src.cols;
int height = src.rows;
for (int i = 0; i < width / 2; i++) {
for (int j = 0; j < height / 2; j++) {
if (sqrt(i * i + j * j) <= pass_start * height / 2|| sqrt(i * i + j * j)>= pass_end * height / 2) {
map[i][j] = 0;
map[width - i - 1][j] = 0;
map[i][height - j - 1] = 0;
map[width - i - 1][height - j - 1] = 0;
}
}
}
return IDFT(map);
}Show

问题三十六:JPEG 压缩——第一步:离散余弦变换(Discrete Cosine Transformation)
imori.jpg灰度化之后,先进行离散余弦变换,再进行离散余弦逆变换吧!
离散余弦变换(Discrete Cosine Transformation)是一种使用下面式子计算的频率变换:

离散余弦逆变换(Inverse Discrete Cosine Transformation)是离散余弦变换的逆变换,使用下式定义。
在这里,$K$是决定图像复原时分辨率高低的参数。$K=T$时,DCT的系数全被保留,因此IDCT时分辨率最大。$K=1$或$K=2$时,图像复原时的信息量(DCT系数)减少,分辨率降低。如果适当地设定$K$,可以减小文件大小。

在这里我们先将图像分割成$8\times8$的小块,在各个小块中使用离散余弦变换编码,使用离散余弦逆变换解码,这就是 JPEG的编码过程。现在我们也同样地,把图像分割成$8\times8$的小块,然后进行离散余弦变换和离散余弦逆变换。
这一整段我整体都在瞎**译,原文如下:
ここでは画像を8x8ずつの領域に分割して、各領域で以上のDCT, IDCTを繰り返すことで、JPEG符号に応用される。 今回も同様に8x8の領域に分割して、DCT, IDCTを行え。
——gzr
问题三十七:PSNR
离散余弦逆变换中如果不使用$8$作为系数,而是使用$4$作为系数的话,图像的画质会变差。来求输入图像和经过离散余弦逆变换之后的图像的峰值信噪比吧!再求出离散余弦逆变换的比特率吧!
峰值信噪比(Peak Signal to Noise Ratio)缩写为PSNR,用来表示信号最大可能功率和影响它的表示精度的破坏性噪声功率的比值,可以显示图像画质损失的程度。
峰值信噪比越大,表示画质损失越小。峰值信噪比通过下式定义。MAX表示图像点颜色的最大数值。如果取值范围是$[0,255]$的话,那么MAX的值就为255。MSE表示均方误差(Mean Squared Error),用来表示两个图像各个像素点之间差值平方和的平均数:
$$
\text{PSNR}=10\ \log{10}\ \frac{{v{max}}^2}{\text{MSE}}\
\text{MSE}=\frac{\sum\limits{y=0}^{H-1}\ \sum\limits{x=0}^{W-1}\ [I_1(x,y)-I_2(x,y)]^2}{H\ W}
$$
如果我们进行$8\times8$的离散余弦变换,离散余弦逆变换的系数为$KtimesK$的话,比特率按下式定义:
$$
\text{bit rate}=8\ \frac{K^2}{8^2}
$$