问题二十一至问题三十

关于直方图的几个操作的中文翻译一直都十分混乱（成龙抓头.jpg）。下面是我查了资料做的一个对照表。我自己也不是很确定，仅供参考：

中文	English	日本語	具体作用
直方图匹配（规定化）	Histogram Matching ( Specification )	ヒストグラムマッチング	将两张图像的累积分布函数调为一样
直方图均衡化	Histogram Equalization	ヒストグラム均等化（平坦化）	拉开灰度差别，增强对比度
直方图归一化	Histogram Normalization	ヒストグラム正規化	将直方图所有分量限制在一定范围

问题二十一：直方图归一化（ Histogram Normalization ）

来归一化直方图吧。

有时直方图会偏向一边。

比如说，数据集中在$0$处（左侧）的图像全体会偏暗，数据集中在$255$处（右侧）的图像会偏亮。

如果直方图有所偏向，那么其动态范围（ dynamic range ）就会较低。

为了使人能更清楚地看见图片，让直方图归一化、平坦化是十分必要的。

这种归一化直方图的操作被称作灰度变换（Grayscale Transformation）。像素点取值范围从$[c,d]$转换到$[a,b]$的过程由下式定义。这回我们将MARKDOWN_HASHcddf1f424e6ef89f3c7af3e98cedc79aMARKDOWNHASH的灰度扩展到$[0, 255]$范围：
$$
x{out}=
\begin{cases}
a& (\text{if}\quad x{in}<c)\
\frac{b-a}{d-c}\ (x{in}-c)+a&(\text{else if}\quad c\leq x_{in}<d)\
b&(\text{else})
\end{cases}
$$

Answer

void HistogramNormalization(Mat& src,int start=0,int end=255) {
    if (!src.data) return;
    Mat chs[3];
    split(src, chs);
    double maxItem[3], minItem[3];
    for(int i=0;i<3;i++)
        minMaxLoc(chs[i],&minItem[i],&maxItem[i],0,0);
    src.forEach<Vec3b>([&](Vec3b& pix, const int *position) {
        int channal = src.channels();
        for (int c = 0; c < channal; c++) {
            if (pix[c]<minItem[c]) pix[c]=start;
            else if(pix[c] > maxItem[c]) pix[c] = end;
            else pix[c] = ((end - start) / (maxItem[c] - minItem[c])*pix[c] + start);
        }
    });
}

Show

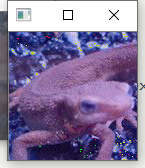
以及两个直方图比较

Note

• 在一个Mat中寻找最大值最小值可以使用minMaxLoc()

问题二十二：直方图操作

让直方图的平均值$m_0=128$，标准差$s_0=52$​吧！

这里并不是变更直方图的动态范围，而是让直方图变得平坦。

可以使用下式将平均值为$m$标准差为$s$的直方图变成平均值为$m_0$标准差为$s0$的直方图：
$$
x{out}=\frac{s0}{s}\ (x{in}-m)+m_0
$$

Answer

void modifyMeanAndStandardDeviation(Mat& src,double mean, double sigma) {
    Mat chs[3];
    split(src, chs);
    Mat meanItem[3], devItem[3];
    for (int i = 0; i < 3; i++)
        meanStdDev(chs[i], meanItem[i], devItem[i]);
    src.forEach<Vec3b>([&](Vec3b& pix, const int *position) {
        int channal = src.channels();
        for (int c = 0; c < channal; c++) {
            pix[c] = (sigma / devItem[c].at<double>(0, 0))*(pix[c] - meanItem[c].at<double>(0, 0)) + mean;
        }
    });
}

Show

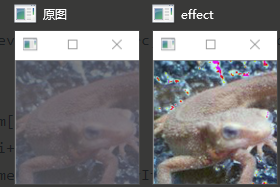
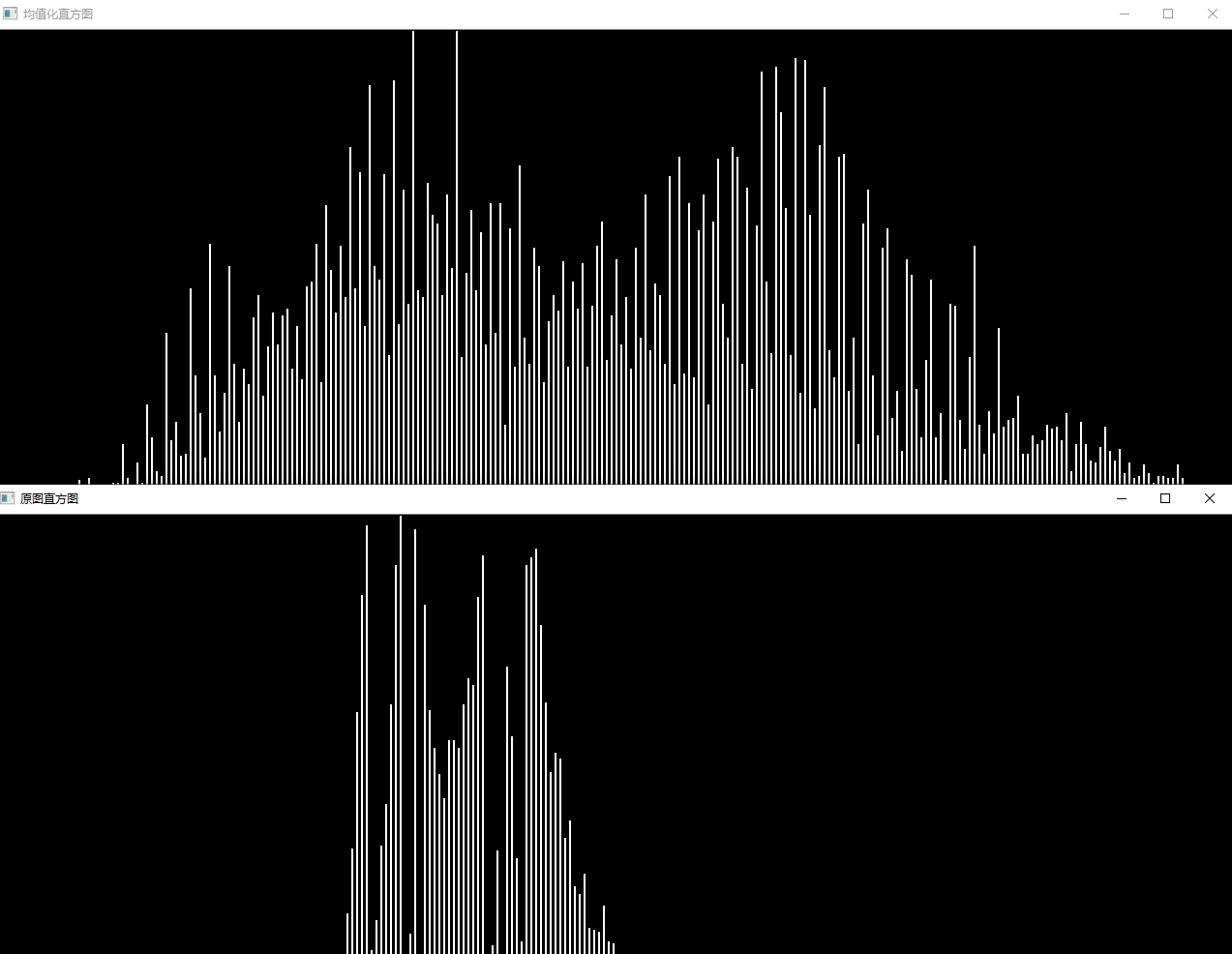
Note

求Mat的均值可以使用如下代码求

Mat mean,dev;
meanStdDev(src,mean,dev);
meam.at<double>(0,0);//均值
dev.at<double>(0,0);//标准差

问题二十三：直方图均衡化（ Histogram Equalization ）

来让均匀化直方图吧！

直方图均衡化是使直方图变得平坦的操作，是不需要计算上面的问题中的平均值、标准差等数据使直方图的值变得均衡的操作。

均衡化操作由以下式子定义。$S$是总的像素数；$Z{max}$是像素点的最大取值（在这里是$255$）；$h(z)$表示取值为$z$的累积分布函数：
$$
Z' = \frac{Z{max}}{S} \ \sum\limits_{i=0}^z\ h(i)
$$

Answer

void HistogramEqualization(Mat& src, uchar maxValue = 255) {
    int gross = src.channels()*src.cols*src.rows;
    double hist[255] = { 0.0 };
    int channal = src.channels();
    src.forEach<Vec3b>([&](Vec3b& pix, const int* position) {
        for (int c = 0; c < channal; c++){
            hist[pix[c]] += 1;
        }
    });
    src.forEach<Vec3b>([&](Vec3b& pix, const int * position) {
        for (int c = 0; c < channal; c++) {
            int cur_vaule = pix[c];
            int hist_sum = 0;
            for (int i = 0; i < cur_vaule; i++) hist_sum += hist[i];
            pix[c] = (int)((float)maxValue *(float)hist_sum / (float)gross);
        }
    });
}

Show

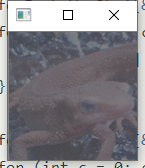
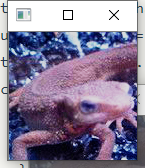
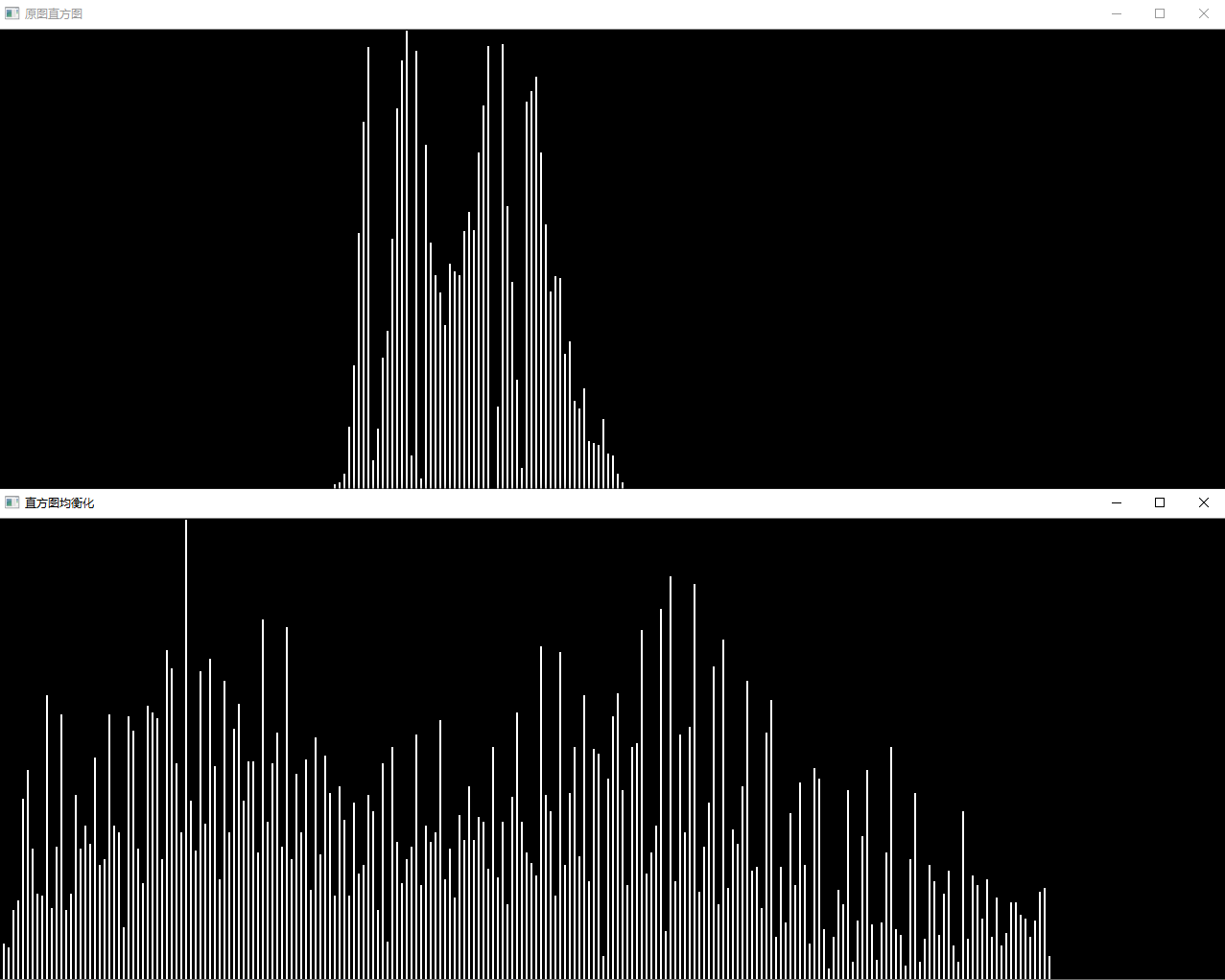
Note

• $\sum\limits_{i=0}^z\ h(i)$可以提前在循环外面计算好,通过查表的方式得到结果可以有效提升计算速度

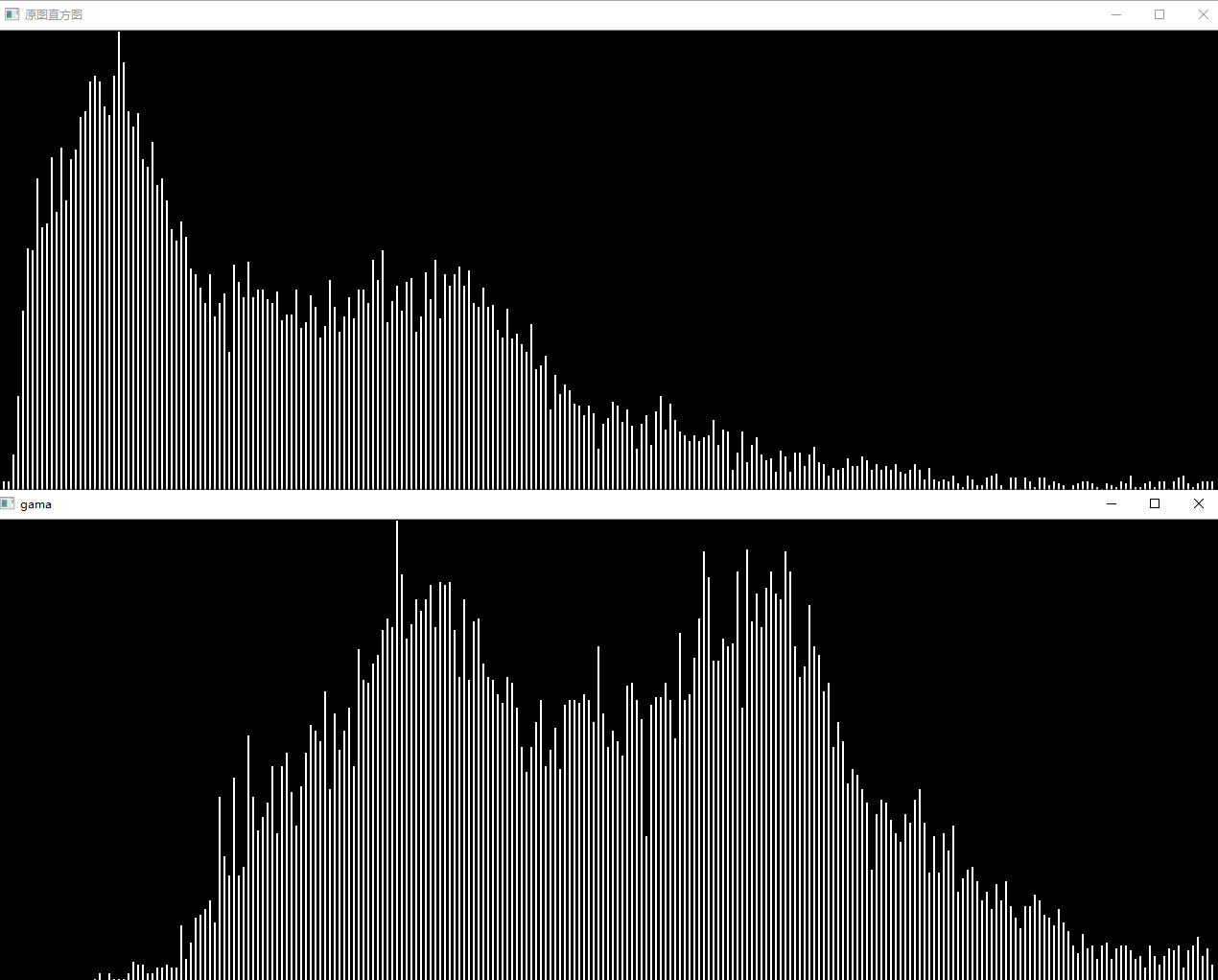
问题二十四：伽玛校正（Gamma Correction）¹

对imori_gamma.jpg进行伽马校正（$c=1$，$g=2.2$）吧！

伽马校正用来对照相机等电子设备传感器的非线性光电转换特性进行校正。如果图像原样显示在显示器等上，画面就会显得很暗。伽马校正通过预先增大 RGB 的值来排除显示器的影响，达到对图像修正的目的。

由于下式引起非线性变换，在该式中，$x$被归一化，限定在$[0,1]$范围内。$c$是常数，$g$为伽马变量（通常取$2.2$）：
$$
x' = c\ {I{in}}^ g
$$
因此，使用下面的式子进行伽马校正：
$$
I{out} ={\frac{1}{c}\ I_{in}} ^ {\frac{1}{g}}
$$

Principle

• Why
  人眼对外界光源的感光值与输入光强不是呈线性关系的，而是呈指数型关系的。在低照度下，人眼更容易分辨出亮度的变化，随着照度的增加，人眼不易分辨出亮度的变化。
  而摄像机感光与输入光强呈线性关系。
• How
  假设图像中有一个像素，值是 200 ，那么对这个像素进行校正必须执行如下步骤： 
  　　1. 归一化 ：将像素值转换为  0 ～ 1  之间的实数。 算法如下 : ( i + 0. 5)/256  这里包含 1 个除法和 1 个加法操作。对于像素  A  而言  , 其对应的归一化值为  0. 783203 。 

　　2. 预补偿 ：根据公式  , 求出像素归一化后的 数据以  1 /gamma  为指数的对应值。这一步包含一个 求指数运算。若  gamma  值为  2. 2 ,  则  1 /gamma  为  0. 454545 , 对归一化后的  A  值进行预补偿的结果就 是  0. 783203 ^0. 454545 = 0. 894872 。 

　　3. 反归一化 ：将经过预补偿的实数值反变换为  0  ～  255  之间的整数值。具体算法为 : f*256 - 0. 5  此步骤包含一个乘法和一个减法运算。续前 例  , 将  A  的预补偿结果  0. 894872  代入上式  , 得到  A  预补偿后对应的像素值为  228 , 这个  228  就是最后送 入显示器的数据。

Answer

void GammaCorrection(Mat& src, int coefficient = 1, double gama = 2.2) {
    int channel = src.channels();

    double normalizationMap[256];//通过查表的方式归一化
    for (int i = 0; i < 256; i++) {
        normalizationMap[i] = (i + 0.5) / 256;
    }

    //补偿
    src.forEach<Vec3b>([&](Vec3b& pix, const int * position) {
        for (int c = 0; c < channel; c++) {
            double after_normal = normalizationMap[pix[c]];//归一化结果
            double effect = coefficient*pow(after_normal, 1/gama);
            pix[c] = (uchar)(effect * 256 - 0.5);
        }
    });

}

Show

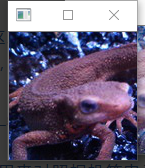
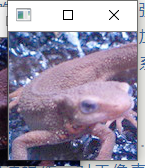
问题二十五：最邻近插值（ Nearest-neighbor Interpolation ）

使用最邻近插值将图像放大$1.5$倍吧！

最近邻插值在图像放大时补充的像素取最临近的像素的值。由于方法简单，所以处理速度很快，但是放大图像画质劣化明显。

使用下面的公式放大图像吧！$I'$为放大后图像，$I$为放大前图像，$a$为放大率，方括号是四舍五入取整操作：

$$
I'(x,y) = I([\frac{x}{a}], [\frac{y}{a}])
$$

Answer

//最邻近插值的方法放大图像
void Nearest_neighborInterpolation(Mat&src, double times) {
    Mat result = Mat::zeros(src.rows*times, src.cols*times, CV_8UC3);
    result.forEach<Vec3b>([&](Vec3b& pix, const int * position) {
        int x = position[0];
        int y = position[1];
        int target_x = (double)x / (times);
        int target_y = (double)y / (times);
        for (int c = 0; c < 3; c++) {
            pix[c] = src.at<Vec3b>(target_x, target_y)[c];
        }
    });
    src=result;
}

Show

Note

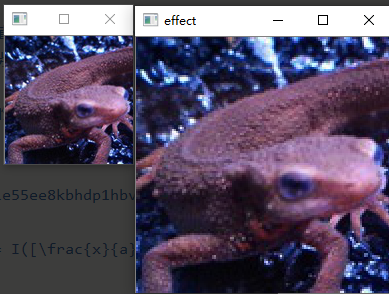
放大后有明显马赛克痕迹,可以尝试加入之前习题中的滤波器
以下为放大6倍并均值滤波效果

问题二十六：双线性插值（ Bilinear Interpolation ）

使用双线性插值将图像放大$1.5$倍吧！

双线性插值考察$4$邻域的像素点，并根据距离设置权值。虽然计算量增大使得处理时间变长，但是可以有效抑制画质劣化。

1. 放大后图像的座标$(x',y')$除以放大率$a$，可以得到对应原图像的座标$(\lfloor \frac{x'}{a}\rfloor , \lfloor \frac{y'}{a}\rfloor)$。

2. 求原图像的座标$(\lfloor \frac{x'}{a}\rfloor , \lfloor \frac{y'}{a}\rfloor)$周围$4$邻域的座标$I(x,y)$，$I(x+1,y)$，$I(x,y+1)$，$I(x+1, y+1)$：

   

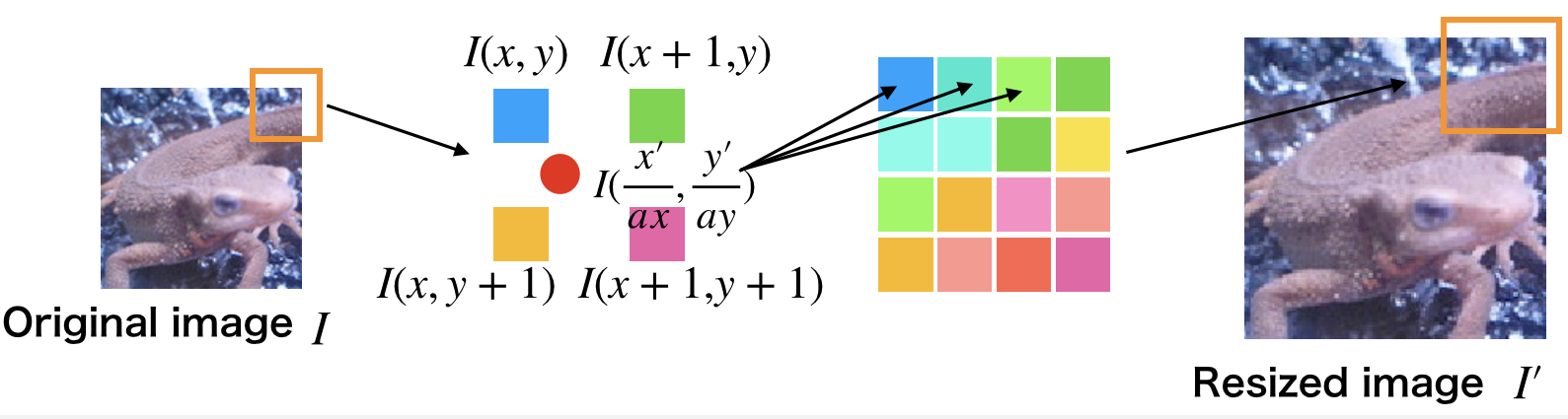
3. 分别求这4个点与$(\frac{x'}{a}, \frac{y'}{a})$的距离，根据距离设置权重：$w = \frac{d}{\sum\ d}$

4. 根据下式求得放大后图像$(x',y')$处的像素值：
   $$
   d_x = \frac{x'}{a} - x\
   d_y = \frac{y'}{a} - y\
   I'(x',y') = (1-d_x)\ (1-d_y)\ I(x,y) + d_x\ (1-d_y)\ I(x+1,y) + (1-d_x)\ d_y\ I(x,y+1) + d_x\ d_y\ I(x+1,y+1)
   $$

Answer

//双线性差值
void BilinearInterpolation(Mat& src, double times) {
    Mat result = Mat::zeros(src.rows*times, src.cols*times, CV_8UC3);
    result.forEach<Vec3b>([&](Vec3b& pix, const int * position) {
        int x = position[0];
        int y = position[1];
        int y_before = (float)y / times;
        y_before = std::min(y_before, src.cols - 1);
        int x_before = (float)x / times;
        x_before = std::min(x_before, src.rows-1);
        double dx = x / times - x_before;
        double dy = y / times - y_before;
        for (int c = 0; c < 3; c++) {
            double val = (1 - dx)*(1 - dy)*src.at<Vec3b>(x_before, y_before)[c] +
                dx * (1 - dy)*src.at<Vec3b>(x_before + 1, y_before)[c] +
                (1 - dx)*(dy)*src.at<Vec3b>(x_before, y_before + 1)[c] +
                dx * dy*src.at<Vec3b>(x_before + 1, y_before + 1)[c];
            pix[c] = (uchar)val;
        }
    });
    src = result;
}

Show

这里是放大了6倍

问题二十七：双三次插值（ Bicubic Interpolation ）

使用双三次插值将图像放大$1.5$倍吧！

双三次插值是双线性插值的扩展，使用邻域$16$像素进行插值。

各自像素间的距离由下式决定：
$$
\begin{align}
d_{x1} = |\frac{x'}{a\ x} - (x-1)|\quad
d{x2} = |\frac{x'}{a\ x}- x| \quad
d{x3} = |\frac{x'}{a\ x}- (x+1)|\quad
d{x4} = |\frac{x'}{a\ x} - (x+2)|\
d{y1} = |\frac{x'}{a\ y} - (y-1)|\quad
d{y2} = |\frac{x'}{a\ y} - y| \quad
d{y3} = |\frac{x'}{a\ y} - (y+1)| \quad
d{y_4} = |\frac{x'}{a\ y} - (y+2)|
\end{align}
$$
权重由基于距离的函数取得。$a$在大部分时候取$-1$。大体上说，图中蓝色像素的距离$|t|\leq 1$，绿色像素的距离$1<|t|\leq 2$：
$$
h(t)=
\begin{cases}
(a+2)\ |t|^3 - (a+3)\ |t|^2 + 1 &\text{when}\quad |t|\leq 1 \
a\ |t|^3 - 5\ a\ |t|^2 + 8\ a\ |t| - 4\ a&\text{when}\quad 1<|t|\leq 2\
0&\text{else}
\end{cases}
$$
利用上面得到的权重，通过下面的式子扩大图像。将每个像素与权重的乘积之和除以权重的和。
$$
I'(x', y')=\frac{1}{\sum\limits{j=1}^4\ \sum\limits{i=1}^4\ h(d{xi})\ h(d{yj})}\ \sum\limits{j=1}^4\ \sum\limits{i=1}^4\ I(x+i-2,y+j-2)\ h(d{xi})\ h(d{yj})
$$

问题二十八：仿射变换（ Afine Transformations ）——平行移动

以下公式中有些矩阵乘法左右是反的,原文中便是如此,这里未做更改,无法相乘的部分需要大家自己做纠正.

利用仿射变换让图像在$x$方向上$+30$，在$y$方向上$-30$吧！

仿射变换利用$3\times3$的矩阵来进行图像变换。

变换的方式有平行移动（问题二十八）、放大缩小（问题二十九）、旋转（问题三十）、倾斜（问题三十一）等。

原图像记为$(x,y)$，变换后的图像记为$(x',y')$。

图像放大缩小矩阵为下式：
$$
\left(
\begin{matrix}
x'\
y'
\end{matrix}
\right)=
\left(
\begin{matrix}
a&b\
c&d
\end{matrix}
\right)\
\left(
\begin{matrix}
x\
y
\end{matrix}
\right)
$$
另一方面，平行移动按照下面的式子计算：
$$
\left(
\begin{matrix}
x'\
y'
\end{matrix}
\right)=
\left(
\begin{matrix}
x\
y
\end{matrix}
\right)+
\left(
\begin{matrix}
t_x\
t_y
\end{matrix}
\right)
$$
把上面两个式子盘成一个：
$$
\left(
\begin{matrix}
x'\
y'\
1
\end{matrix}
\right)=
\left(
\begin{matrix}
a&b&t_x\
c&d&t_y\
0&0&1
\end{matrix}
\right)\
\left(
\begin{matrix}
x\
y\
1
\end{matrix}
\right)
$$
但是在实际操作的过程中，如果一个一个地计算原图像的像素的话，处理后的像素可能没有在原图像中有对应的坐标。²

因此，我们有必要对处理后的图像中各个像素进行仿射变换逆变换，取得变换后图像中的像素在原图像中的坐标。仿射变换的逆变换如下：
$$
\left(
\begin{matrix}
x\
y
\end{matrix}
\right)=
\frac{1}{a\ d-b\ c}\
\left(
\begin{matrix}
d&-b\
-c&a
\end{matrix}
\right)\
\left(
\begin{matrix}
x'\
y'
\end{matrix}
\right)-
\left(
\begin{matrix}
t_x\
t_y
\end{matrix}
\right)
$$
这回的平行移动操作使用下面的式子计算。$t_x$和$t_y$是像素移动的距离。
$$
\left(
\begin{matrix}
x'\
y'\
1
\end{matrix}
\right)=
\left(
\begin{matrix}
1&0&t_x\
0&1&t_y\
0&0&1
\end{matrix}
\right)\
\left(
\begin{matrix}
x\
y\
1
\end{matrix}
\right)
$$

Answer

先根据放射变换定义工具函数,原理就是根据放射变换的逆变换公式得出目标图像某一位置的像素在原图像中对应的位置

$$
\left(
\begin{matrix}
x\
y
\end{matrix}
\right)=
\frac{1}{a\ d-b\ c}\
\left(
\begin{matrix}
d&-b\
-c&a
\end{matrix}
\right)\
\left(
\begin{matrix}
x'\
y'
\end{matrix}
\right)-
\left(
\begin{matrix}
t_x\
t_y
\end{matrix}
\right)
$$

initSingleChannelMat()在之前的题目中有定义过,这里使用该方式初始化矩阵或者用opencv自带的方式都可以

//仿射变换的逆变换
Mat AfineTransformations(Mat& src, double a, double b, double c, double d, double tx, double ty) {
    double  coefficient = 1 / (a*d - b * c);
    double t[4] = {
        d,-b,
        -c,a
    };
    Mat a_ = initSingleChannelMat<double>(t,2, CV_64FC1);

    double t_[2] = {
        tx,
        ty
    };
    Mat b_(Size(1,2), CV_64FC1, t_);
    src.convertTo(src, CV_64FC1);
    Mat step_1 = a_ * src;
    return coefficient * step_1+ b_;
}

在根据平移需要的仿射变换进行变换

//通过放射变换实现平移
void transAT(Mat& src, double tx, double ty) {
    Mat result = Mat::zeros(src.rows, src.cols, CV_8UC3);
    result.forEach<Vec3b>([&](Vec3b& pix, const int * position) {
        int x = position[0];
        int y = position[1];
        int cur_pos[2][17] = { x,y };
        Mat m(Size(1, 2), CV_32SC1, cur_pos);
        Mat ori_pos = AfineTransformations(m, 1, 0, 0, 1, tx, ty);
        //printMat(m);
        for (int i = 0; i < 3; i++) {
            int ori_pos_x = ori_pos.at<Vec<double, 1>>(0, 0)[0];
            int ori_pos_y = ori_pos.at<Vec<double, 1>>( 1,0)[0];
            if (ori_pos_x >= src.rows || ori_pos_y >= src.cols || ori_pos_x < 0 || ori_pos_y < 0) {
                pix[i] = 0;
            }
            else
                pix[i] = src.at<Vec3b>(ori_pos_x, ori_pos_y)[i];
        }
    });
    src = result;
}

Show

Note

• 在进行矩阵乘法运算时要注意两个Mat 的数据类型,比如说CV_64FC1与CV_32SC1之间无法直接相乘,会产生如下错误:
  
  可以使用src.convertTo(src, CV_64FC1);函数来进行主句类型之间的转换.其中src是一个Mat对象的实例.

问题二十九：仿射变换（ Afine Transformations ）——放大缩小

1. 使用仿射变换，将图片在$x$方向上放大$1.3$倍，在$y$方向上缩小至原来的$\frac{4}{5}$。
2. 在上面的条件下，同时在$x$方向上向右平移$30$（$+30$），在$y$方向上向上平移$30$（$-30$）。

Answer

//通过放射变换实现放大和缩小
void amplifyAT(Mat& src, double dx, double dy) {
    Mat result = Mat::zeros(src.rows*dx, src.cols*dy, CV_8UC3);

    result.forEach<Vec3b>([&](Vec3b& pix, const int * position) {
        int x = position[0];
        int y = position[1];
        int cur_pos[2][21] = { x,y };
        Mat m(Size(1, 2), CV_32SC1, cur_pos);
        Mat ori_pos = AfineTransformations(m, dx, 0, 0, dy, 0,0);
        //printMat(m);
        for (int i = 0; i < 3; i++) {
            int ori_pos_x = ori_pos.at<Vec<double, 1>>(0, 0)[0];
            int ori_pos_y = ori_pos.at<Vec<double, 1>>(1, 0)[0];
            if (ori_pos_x >= src.rows || ori_pos_y >= src.cols || ori_pos_x < 0 || ori_pos_y < 0) {
                pix[i] = 0;
            }
            else
                pix[i] = src.at<Vec3b>(ori_pos_x, ori_pos_y)[i];
        }
    });
    src = result;
}

Show

该变换是横向变为2倍,纵向变为0.5倍

问题三十：仿射变换（ Afine Transformations ）——旋转

1. 使用仿射变换，逆时针旋转$30$度。
2. 使用仿射变换，逆时针旋转$30$度并且能让全部图像显现（也就是说，单纯地做仿射变换会让图片边缘丢失，这一步中要让图像的边缘不丢失，需要耗费一些工夫）。

使用下面的式子进行逆时针方向旋转$A$度的仿射变换：

$$
\left(
\begin{matrix}
x'\
y'\
1
\end{matrix}
\right)=
\left(
\begin{matrix}
\cos(A)&-\sin(A)&t_x\
\sin(A)&\cos(A)&t_y\
0&0&1
\end{matrix}
\right)\
\left(
\begin{matrix}
x\
y\
1
\end{matrix}
\right)
$$

Answer

//通过放射变换实现旋转
void rollAT(Mat& src, double angle) {
    Mat result = Mat::zeros(src.rows, src.cols, CV_8UC3);
    angle = 3.1415926*angle /  180;
    result.forEach<Vec3b>([&](Vec3b& pix, const int * position) {
        int x = position[0];
        int y = position[1];
        int cur_pos[2][1] = { x,y };
        Mat m(Size(1,2), CV_32SC1, cur_pos);
        Mat ori_pos = AfineTransformations(m, cos(angle), sin(angle), -sin(angle), cos(angle), 0, 0);
        for (int i = 0; i < 3; i++) {
            int ori_pos_x = ori_pos.at<Vec<double, 1>>(0, 0)[0];
            int ori_pos_y = ori_pos.at<Vec<double, 1>>(1, 0)[0];
            if (ori_pos_x >= src.rows || ori_pos_y >= src.cols || ori_pos_x < 0 || ori_pos_y < 0) {
                pix[i] = 0;
            }
            else
                pix[i] = src.at<Vec3b>(ori_pos_x, ori_pos_y)[i];
        }
    });
    src = result;
}

Show

这里进行逆时针30度的变换

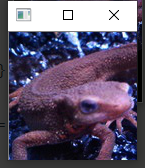
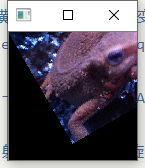
Note

• #include<math.h>中的sin()和cos()函数都是弧度制,可以根据需要进行转换

为图像处理初学者设计的 100 个问题 问题三十一至问题四十

标签（空格分隔）： OpenCV

问题三十一至四十

问题三十一：仿射变换（Afine Transformations）——倾斜

1. 使用仿射变换，输出（1）那样的$x$轴倾斜$30$度的图像（$t_x=30$），这种变换被称为X-sharing。
2. 使用仿射变换，输出（2）那样的y轴倾斜$30$度的图像（$t_y=30$），这种变换被称为Y-sharing。
3. 使用仿射变换，输出（3）那样的$x$轴、$y$轴都倾斜$30$度的图像($t_x = 30$，$t_y = 30$)。

原图像的大小为$h\ w$，使用下面各式进行仿射变换：

Answer

函数AfineTransformations()见上一章

void leanAt(Mat& src, double x_sharing, double y_sharing) {
    Mat result = Mat::zeros(src.rows, src.cols, CV_8UC3);
    result.forEach<Vec3b>([&](Vec3b& pix, const int * position) {
        int x = position[0];
        int y = position[1];
        int cur_pos[2][1] = { x,y };
        Mat m(Size(1, 2), CV_32SC1, cur_pos);
        double a_x = x_sharing / src.rows;
        double a_y = y_sharing / src.cols;
        Mat ori_pos = AfineTransformations(m, 1,a_x,a_y,1, 0, 0);
        //printMat(ori_pos);
        for (int i = 0; i < 3; i++) {
            int ori_pos_x = ori_pos.at<Vec<double, 1>>(0, 0)[0];
            int ori_pos_y = ori_pos.at<Vec<double, 1>>(1, 0)[0];
            if (ori_pos_x >= src.rows || ori_pos_y >= src.cols || ori_pos_x < 0 || ori_pos_y < 0) {
                pix[i] = 0;
            }
            else
                pix[i] = src.at<Vec3b>(ori_pos_x, ori_pos_y)[i];
        }
    });
    src = result;
}

Show

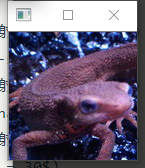
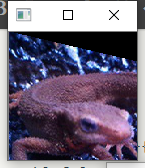
Note

• 利用OpenCV的API进行仿射变换

  • 第一步：获取仿射映射矩阵（两种）

    getAffineTransform()       //三点法
    Mat M1=getAffineTransform(const Point2f* src, const Point2f* dst)
      //参数const Point2f* src：原图的三个固定顶点

    //参数const Point2f dst：目标图像的三个固定顶点
    //返回值：Mat型变换矩阵，可直接用于warpAffine()函数
    //注意，顶点数组长度超过3个，则会自动以前3个为变换顶点；数组可用Point2f[]或Point2f表示

    
    ```cpp
    getRotationMatrix2D       //直接指定比例和角度
    Mat M2=getRotationMatrix2D (CvPoint2D32f  center,double angle,double scale)
        //参数CvPoint2D32f  center，表示源图像旋转中心
        //参数double angle，旋转角度，正值表示逆时针旋转
        //参数double scale，缩放系数

  • 第二步：进行仿射变换

    C++ void warpAffine(InputArray src, OutputArray dst, InputArray M, Size dsize, int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT, const Scalar& borderValue=Scalar())
    //参数InputArray src：输入变换前图像
    //参数OutputArray dst：输出变换后图像，需要初始化一个空矩阵用来保存结果，不用设定矩阵尺寸
    //参数InputArray M：变换矩阵，用另一个函数getAffineTransform()计算
    //参数Size dsize：设置输出图像大小
    //参数int flags = INTER_LINEAR：设置插值方式，默认方式为线性插值(另一种WARP_FILL_OUTLIERS)
    //参数int borderMode=BORDER_CONSTANT：边界像素模式，默认值BORDER_CONSTANT
    //参数const Scalar& borderValue=Scalar()，在恒定边界情况下取的值，默认值为Scalar（），即0

    第五个参数插值方式可选方式：	标识符	含义
    INTER_NEAREST	最邻近插值
    INTER_LINEAR	线性插值(默认)
    INTER_CUBIC	三次样条插值
    INTER_AREA	区域插值
    INTER_LANCZOS4	LancZoc4 插值
    INTER_LINEAR_EXACT	双线性插值
    INTER_MAX	插补码掩码
    WARP_FILL_OUTLIERS	填充所有目标图像像素。如果它们中的一些对应于源图像，它们被设置为0
    WARP_INVERSE_MAP	逆变换

问题三十二：傅立叶变换（Fourier Transform）

使用离散二维傅立叶变换（Discrete Fourier Transformation），将灰度化的imori.jpg表示为频谱图。然后用二维离散傅立叶逆变换将图像复原。

二维离散傅立叶变换是傅立叶变换在图像处理上的应用方法。通常傅立叶变换用于分离模拟信号或音频等连续一维信号的频率。但是，数字图像使用$[0,255]$范围内的离散值表示，并且图像使用$H\times W$的二维矩阵表示，所以在这里使用二维离散傅立叶变换。

二维离散傅立叶变换使用下式计算，其中$I$表示输入图像：
$$
G(k,l)=\frac{1}{H\ W}\ \sum\limits{y=0}^{H-1}\ \sum\limits{x=0}^{W-1}\ I(x,y)\ e^{-2\ \pi\ i\ (\frac{k\ x}{W}+\frac{l\ y}{H})}
$$
在这里让图像灰度化后，再进行离散二维傅立叶变换。

频谱图为了能表示复数$G$，所以图上所画长度为$G$的绝对值。这回的图像表示时，请将频谱图缩放至$[0,255]$范围。

二维离散傅立叶逆变换从频率分量$G$按照下式复原图像：
$$
I(x,y)=\frac{1}{H\ W}\ \sum\limits{l=0}^{H-1}\ \sum\limits{k=0}^{W-1}\ G(l,k)\ e^{2\ \pi\ i\ (\frac{k\ x}{W}+\frac{l\ y}{H})}
$$

上式中$\exp(j)$是个复数，实际编程的时候请务必使用下式中的绝对值形态¹：

如果只是简单地使用for语句的话，计算量达到$128^4$，十分耗时。如果善用NumPy的化，则可以减少计算量（答案中已经减少到$128^2$）。

Principe

本节Principe中的内容适合不了解傅里叶变换的读者阅读

 傅里叶变换可以将一副图片分解为正弦和余弦两个分量，换言之，它可以将一幅图像从空间域（spatial domain）转换为频域（frequency domain）。这种变换的思想是任何函数可以很精确的接近无穷个sin()函数和cos()函数的和。
我们来梳理一下概念：

• 空间域
  一般情况下，空间域的图像是f(x, y) = 灰度级（0-255），形象一点就是一个二维矩阵，每一个坐标对应一个颜色值
• 频率域
  对于一个正弦信号，如果它的幅度变化很快，我们称之为高频信号，如果变化非常慢，我们称之为低频信号。迁移到图像中，图像哪里的幅度变化非常大呢？边界点或者噪声。所以我们说边界点和噪声是图像中的高频分量（这里的高频是指变化非常快，不是出现的次数多），图像的主要部分集中在低频分量。

由于图像变换的结果原点在边缘部分，不容易显示，所以将原点移动到中心部分。
那么结果便是中间一个亮点朝着周围发散开来，越远离中心位置的能量越低（越暗）。

对于二位图像其傅里叶变换公式如下：
$$
F(k,l)= \sum\limits{y=0}^{N-1}\ \sum\limits{x=0}^{N-1}\ f(x,y)\ e^{-2\ \pi\ j\ (\frac{k\ x}{N}+\frac{l\ y}{N})}
$$
$$
e^{ix}=cos x+i sin x
$$
式中 f(i, j)是图像空间域的值，F(k ,l)是频域的值。傅里叶转换的结果是复数，这也显示了傅里叶变换是一幅实数图像和虚数图像叠加或者是幅度图像和相位图像叠加的结果。

Answer

toGray()函数在之第一章声明过,也可是使用OpenCV自带的API来转换灰度图

• 傅里叶变换

  //// Discrete Fourier transformation
  //这个奇怪的vector就是用来存转换后的频域的
  std::vector<
  std::vector<
  std::complex<double>>> DFT(Mat& src) {
  int width = src.cols;
  int height = src.rows;
  std::complex<double> val;
  Mat grey = toGray(src);
  std::vector<std::vector<std::complex<double>>> FTMap;
  Mat result = Mat::zeros(width, height, CV_8UC1);
  
  //j,k用来表示频谱图中的坐标
  for (int j = 0; j < width; j++) {
      std::vector<std::complex<double>> MapLine;
      for (int k = 0; k < height; k++) {
          val.real(0);
          val.imag(0);
  
          //x,y表示时域中的坐标
          for (int x = 0; x < width; x++) {
              for (int y = 0; y < height; y++) {
                  uchar I = grey.at<Vec<uchar, 1>> (x, y)[0];
                  double theta = (double)-2 * 3.1415926*(((double)k*(double)y / (double)height) + ((double)j*(double)x / (double)width));
                  val += (double)I*std::complex<double>(cos(theta), sin(theta));
              }
          }
          val /= sqrt((double)width*(double)height);
          result.at<Vec<uchar, 1>>(j, k)[0] = (uchar)sqrt(val.imag()*val.imag() + val.real()*val.real());
          MapLine.push_back(val);
      }
      FTMap.push_back(MapLine);
  }
  //输出以下现在是什么样的图案
  imshow("FDT", result);
  return FTMap;
  }

• 傅里叶逆变换

  Mat IDFT(std::vector<std::vector<std::complex<double>>> FTMap) {
  Mat result = Mat::zeros(128, 128, CV_8UC1);
  int width=128, height = 128;
  
  std::complex<double> val;
  
  for (int j = 0; j < width; j++) {
      std::vector<std::complex<double>> MapLine;
      for (int k = 0; k < height; k++) {
          val.real(0);
          val.imag(0);
  
          //x,y表示时域中的坐标
          for (int x = 0; x < width; x++) {
              for (int y = 0; y < height; y++) {
                  std::complex<double> G = FTMap[x][y];
                  double theta = (double)2 * 3.1415926*(((double)k*(double)y / (double)height) + ((double)j*(double)x / (double)width));
                  val += G*std::complex<double>(cos(theta), sin(theta));
              }
          }
          result.at<Vec<uchar, 1>>(j, k)[0] = (uchar)(std::abs(val) / sqrt(height * width));
      }
  }
  return result;

• 在main函数中这样调用就可以了

  Mat img = imread("G:\\cv\\ImageProcessing100Wen-master\\Question_21_30\\imori.jpg");
  imshow("原图", img);
  imshow("effect",IDFT(DFT(img)));

SHow

• 原图
  

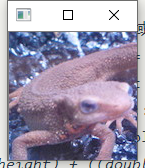
• 转换后的频域图
  

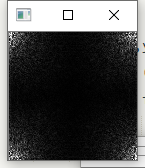
• 逆变换的复原图
  

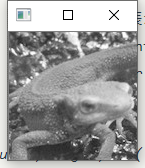
Note

• 可以看到这种方法来求傅里叶变换以及傅里叶逆变换的时间复杂度非常高,达到$O(n^4)$,所以常用的方法是FFT,ji快速傅里叶变换,在之后的题目中会介绍到

问题三十三：傅立叶变换——低通滤波

将imori.jpg灰度化之后进行傅立叶变换并进行低通滤波，之后再用傅立叶逆变换复原吧！

通过离散傅立叶变换得到的频率在左上、右上、左下、右下等地方频率较低，在中心位置频率较高。²

在图像中，高频成分指的是颜色改变的地方（噪声或者轮廓等），低频成分指的是颜色不怎么改变的部分（比如落日的渐变）。在这里，使用去除高频成分，保留低频成分的低通滤波器吧！

在这里，假设从低频的中心到高频的距离为$r$，我们保留$0.5\ r$​的低频分量。

Answer

傅里叶变换和逆变换在前面已经实现过了,这一题直接调用

//低频滤波
Mat LowPassFilter(Mat& src, double pass_r) {
auto map = DFT(src);
int width = src.cols;
int height = src.rows;
for (int i = 0; i < width/2; i++) {
for (int j = 0; j < height/2; j++) {
if (sqrt(i * i + j * j) >= pass_r * height / 2) {
map[i][j] = 0;
map[width - i-1][j] = 0;
map[i][height - j-1] = 0;
map[width - i - 1][height - j - 1] = 0;
}
}
}
return IDFT(map);
}

Show

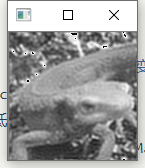
问题三十四：傅立叶变换——高通滤波

将imori.jpg灰度化之后进行傅立叶变换并进行高通滤波，之后再用傅立叶逆变换复原吧！

在这里，我们使用可以去除低频部分，只保留高频部分的高通滤波器。假设从低频的中心到高频的距离为$r$，我们保留$0.2\ r$​的低频分量。

Answer

//高通滤波
Mat HighPassFilter(Mat& src, double pass_r) {
    auto map = DFT(src);
    int width = src.cols;
    int height = src.rows;
    for (int i = 0; i < width / 2; i++) {
        for (int j = 0; j < height / 2; j++) {
            if (sqrt(i * i + j * j) <= pass_r * height / 2) {
                map[i][j] = 0;
                map[width - i - 1][j] = 0;
                map[i][height - j - 1] = 0;
                map[width - i - 1][height - j - 1] = 0;
            }
        }
    }
    return IDFT(map);
}

Show

问题三十五：傅立叶变换——带通滤波

将imori.jpg灰度化之后进行傅立叶变换并进行带通滤波，之后再用傅立叶逆变换复原吧！

在这里，我们使用可以保留介于低频成分和高频成分之间的分量的带通滤波器。在这里，我们使用可以去除低频部分，只保留高频部分的高通滤波器。假设从低频的中心到高频的距离为$r$，我们保留$0.1\ r$至$0.5\ r$的分量。

Answer

//带通滤波
Mat BandPassFilter(Mat& src, double pass_start, double pass_end) {
    auto map = DFT(src);
    int width = src.cols;
    int height = src.rows;
    for (int i = 0; i < width / 2; i++) {
        for (int j = 0; j < height / 2; j++) {
            if (sqrt(i * i + j * j) <= pass_start * height / 2|| sqrt(i * i + j * j)>= pass_end * height / 2) {
                map[i][j] = 0;
                map[width - i - 1][j] = 0;
                map[i][height - j - 1] = 0;
                map[width - i - 1][height - j - 1] = 0;
            }
        }
    }
    return IDFT(map);
}

Show

问题三十六：JPEG 压缩——第一步：离散余弦变换（Discrete Cosine Transformation）

imori.jpg灰度化之后，先进行离散余弦变换，再进行离散余弦逆变换吧！

离散余弦变换（Discrete Cosine Transformation）是一种使用下面式子计算的频率变换：

离散余弦逆变换（Inverse Discrete Cosine Transformation）是离散余弦变换的逆变换，使用下式定义。

在这里，$K$是决定图像复原时分辨率高低的参数。$K=T$时，DCT的系数全被保留，因此IDCT时分辨率最大。$K=1$或$K=2$时，图像复原时的信息量（DCT系数）减少，分辨率降低。如果适当地设定$K$，可以减小文件大小。

在这里我们先将图像分割成$8\times8$的小块，在各个小块中使用离散余弦变换编码，使用离散余弦逆变换解码，这就是 JPEG的编码过程。现在我们也同样地，把图像分割成$8\times8$的小块，然后进行离散余弦变换和离散余弦逆变换。

这一整段我整体都在瞎**译，原文如下：

ここでは画像を8x8ずつの領域に分割して、各領域で以上のDCT, IDCTを繰り返すことで、JPEG符号に応用される。 今回も同様に8x8の領域に分割して、DCT, IDCTを行え。

——gzr

问题三十七：PSNR

离散余弦逆变换中如果不使用$8$作为系数，而是使用$4$作为系数的话，图像的画质会变差。来求输入图像和经过离散余弦逆变换之后的图像的峰值信噪比吧！再求出离散余弦逆变换的比特率吧！

峰值信噪比（Peak Signal to Noise Ratio）缩写为PSNR，用来表示信号最大可能功率和影响它的表示精度的破坏性噪声功率的比值，可以显示图像画质损失的程度。

峰值信噪比越大，表示画质损失越小。峰值信噪比通过下式定义。MAX表示图像点颜色的最大数值。如果取值范围是$[0,255]$的话，那么MAX的值就为255。MSE表示均方误差（Mean Squared Error），用来表示两个图像各个像素点之间差值平方和的平均数：
$$
\text{PSNR}=10\ \log{10}\ \frac{{v{max}}^2}{\text{MSE}}\
\text{MSE}=\frac{\sum\limits{y=0}^{H-1}\ \sum\limits{x=0}^{W-1}\ [I_1(x,y)-I_2(x,y)]^2}{H\ W}
$$
如果我们进行$8\times8$的离散余弦变换，离散余弦逆变换的系数为$KtimesK$的话，比特率按下式定义：
$$
\text{bit rate}=8\ \frac{K^2}{8^2}
$$